Ocean Software Stack

The Ocean software stack provides a chain of tools that implements the steps needed to solve your problem on a CPU/GPU or a D-Wave system. As described in the Workflow Steps: Formulation and Sampling section, these steps include formulating the problem in a way the quantum computer understands (as a binary quadratic model) and solving the formulated problem by submitting it to a D-Wave system or classical sampler (the component used to minimize a BQM and therefore solve the original problem).

It’s helpful to visualize the tool chain as layers of abstraction, each of which handles one part of the solution procedure.

Abstraction Layers

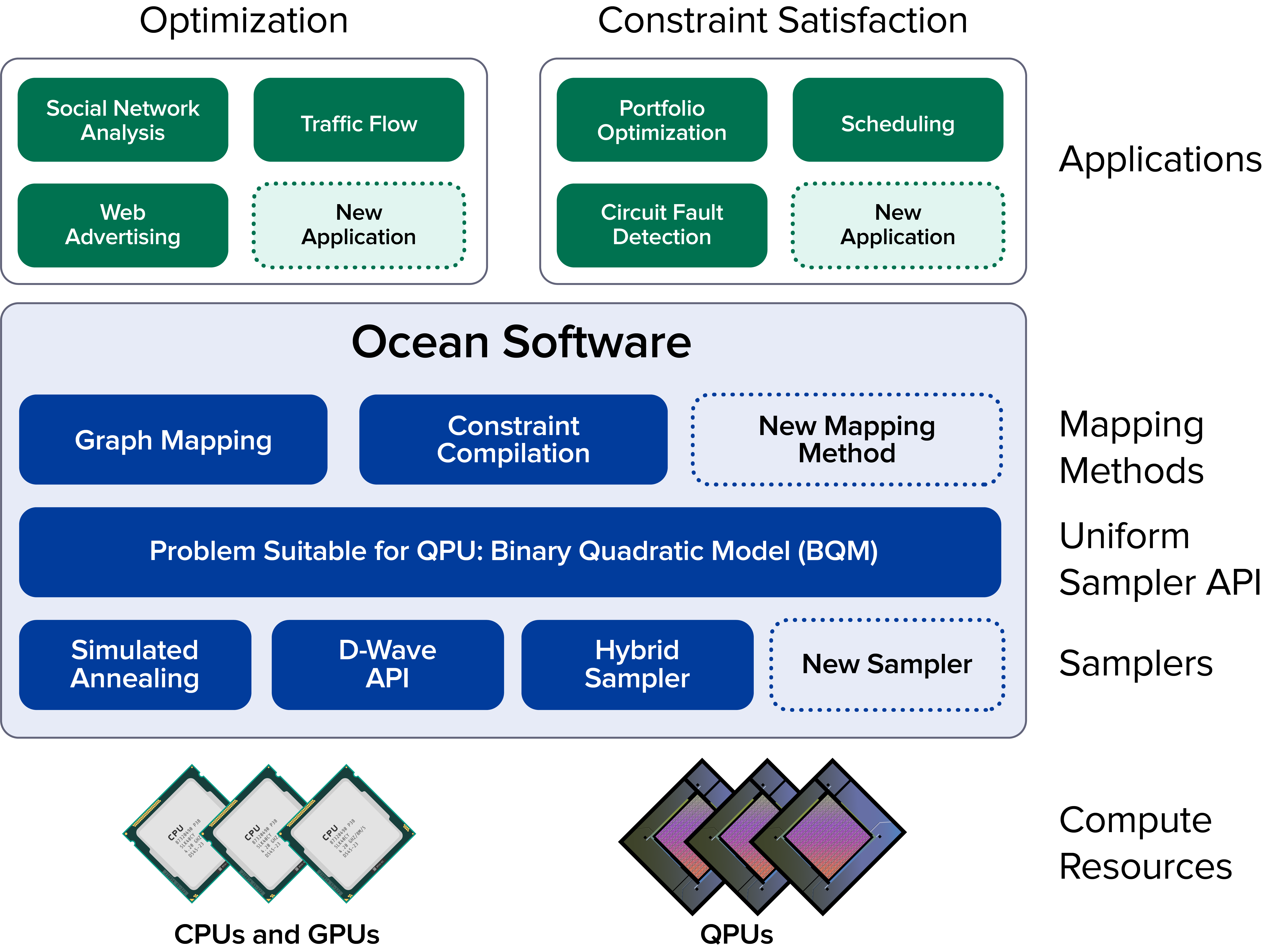
Ocean Software Stack

The Ocean Software Stack graphic above divides Ocean software and its context into the following layers of functionality:

• Compute Resources

  The hardware on which the problem is solved. This might be a D-Wave quantum processor but it can also be the CPU of your laptop computer.

• Samplers

  Abstraction layer of the sampler functionality. Ocean tools implement several samplers that use the D-Wave system and classical compute resources. You can use the Ocean tools to customize a D-Wave sampler, create your own sampler, or use existing (classical) samplers to your code as you develop it.

• Sampler API

  Abstraction layer that represents the problem in a form that can access the selected sampler; for example, a dimod binary quadratic model (BQM) class representing your problem wrapped in a minor-embedding composite that handles the mapping between your problem’s variables and the sampler’s graph.

• Methods

  Tools that help formulate a problem as binary quadratic models; for example dwave_networkx (repo) for graph-related problems.

• Application

  Original problem in its context (“problem space”); for example, circuit fault diagnosis attempts to identify failed logic gates during chip manufacturing.

Problem-to-Solution Tool Chain

As described in the Workflow Steps: Formulation and Sampling section, problems can be posed in a variety of formulations; the D-Wave system solves binary quadratic models. Ocean tools assist you in converting the problem from its original form to a form native to the D-Wave system and sending the compatible problem for solving.

This section will familiarize you with the different tools and how you can fit them together to solve your problem.

Bottom-Up Approach

One approach to envisioning how you can map your problem-solving process to Ocean software is to start from the bottom—the hardware doing the computations—and work your way up the Ocean stack to see the complete picture. This section shows how you might map each stage of the process to a layer of the Ocean stack.

1. Compute resource

   You will likely use some combination of both local classical resources and a D-Wave system in your work with Ocean software. When would you use which?

   • CPU/GPU: for offline testing, small problems that can be solved exactly or heuristically in a reasonable amount of time.

   • QPU: hard problems or for learning how to use quantum resources to solve such problems.

   • Hybrid of both QPU and CPU/GPU: large, complex problems that need to run classically but may benefit from having some parts allocated to a quantum computer for solution.

2. Sampler

   Your sampler provides access to the compute resource that solves your problem.

   The table below shows some Ocean samplers and considerations for selecting one or another.

   Ocean Samplers

   Computation	Tool & Sampler	Usage	Notes
   Classical	dimod ExactSolver	Find all states for small (<20 variables) problems.	For code-development testing.
   Classical	dimod RandomSampler	Random sampler for testing.	For code-development testing.
   Classical	dimod SimulatedAnnealingSampler	Simulated annealing sampler for testing.	For code-development testing.
   Classical	dwave-samplers SteepestDescentSolver.	A steepest-descent solver for binary quadratic models.	For post-processing and convex problems.
   Classical	dwave-samplers SimulatedAnnealingSampler	Simulated annealing sampler.
   Quantum	dwave-system DWaveSampler	Quick incorporation of the D-Wave system as a sampler.	Typically part of a composite that handles minor-embedding.
   Quantum	dwave-system DWaveCliqueSampler	Quick incorporation of the D-Wave system as a sampler.	Handles minor-embedding for clique (complete graph) problems.
   Quantum	dwave-cloud-client Solver()	D-Wave system as a sampler.[1]	For low-level control of problem submission.
   Hybrid	dwave-hybrid KerberosSampler	dimod-compatible hybrid asynchronous decomposition sampler.	For problems of arbitrary structure and size.
   Hybrid	Leap‘s LeapHybridNLSampler	Cloud-based quantum-classical hybrid solver.	For application problems formulated as nonlinear models.
   Hybrid	Leap‘s LeapHybridCQMSampler	Cloud-based quantum-classical hybrid solver.	For constrained quadratic models (CQM) of arbitrary structure and size.
   	dimod custom	Write a custom sampler for special cases.	See examples in dimod.

[1]

This sampler is for low-level work on communicating with SAPI and is not a dimod sampler.

3. Pre- and Post-Processing

   Samplers can be composed of composite patterns that layer pre- and post-processing to binary quadratic programs without changing the underlying sampler.

   The table below shows some Ocean composites and considerations for selecting one or another.

   Ocean Composites

   Tool & Composite	Usage	Notes
   dwave-system EmbeddingComposite	Maps unstructured problems to a structured sampler.	Enables quick incorporation of the D-Wave system as a sampler by handling the minor-embedding to the QPU’s Chimera topology of qubits.
   dwave-system FixedEmbeddingComposite	Maps unstructured problems to a structured sampler.	Uses a pre-calculated minor-embedding for improved performance.
   dwave-system TilingComposite	Tiles small problems multiple times to a Chimera-structured sampler.	Enables parallel sampling for small problems.
   dimod TrackingComposite	Tracks inputs and outputs.	Helps with testing and debugging.
   dwave-preprocessing SpinReversalTransformComposite	Applies spin reversal transform preprocessing.	Improves QPU results by reducing the impact of possible analog and systematic errors.
   dimod StructureComposite	Creates a structured composed sampler from an unstructured sampler.	Maps from a problem graph (e.g., a square graph) to a sampler’s graph.

   In addition to composites that provide pre- and post-processing, Ocean also provides stand-alone tools to handle complex or large problems. For example:

   • minorminer for minor-embedding might be used to improve solutions by fine tuning parameters or incorporating problem knowledge into the embedding.

   • dwave-samplers provides a steepest-descent solver for binary quadratic models that can be run on the samples returned from solvers such as DWaveSampler to find local minima in the neighbourhoods

   • dwave-hybrid splits problems too large for the QPU into pieces solved either via a D-Wave system or a classical solver.

4. Map to a Supported Format

   Typically, you formulate your problem as a binary quadratic model (BQM), which you solve by submitting to the sampler (with its pre- and post-processing composite layers) you select based on the considerations listed above.

   Ocean provides tools for formulating the BQM:

   • dwavebinarycsp for constraint satisfaction problems with small constraints over binary variables. For example, many problems can be posed as satisfiability problems or with Boolean logic.

   • dwave_networkx for implementing graph-theory algorithms of the D-Wave system. Many problems can be posed in a form of graphs—this tool handles the construction of BQMs for several standard graph algorithms such as maximum cut, cover, and coloring.

   You might formulate a BQM mathematically; see Boolean NOT Gate for a mathematical formulation for a two-variable problem.

   See the system documents for more information on techniques for formulating problems as BQMs.

5. Formulate

   The first step in solving a problem is to express it in a mathematical formulation. For example, the Map Coloring problem is to assign a color to each region of a map such that any two regions sharing a border have different colors. To begin solving this problem on any computer, classical or quantum, it must be concretely defined; an intuitive approach, for the map problem, is to think of the regions as variables representing the possible set of colors, the values of which must be selected from some numerical scheme, such as natural numbers.

   The selection function must express the problem’s constraints:

   • Each region is assigned one color only, of C possible colors.

   • The color assigned to one region cannot be assigned to adjacent regions.

   Now solving the problem means finding a permissible value for each of the variables.

   When formulating a problem for the D-Wave system, bear in mind a few considerations:

   • Mathematical formulations must use binary variables because the solution is implemented physically with qubits, and so must translate to spins \(s_i \in {−1, +1}\) or equivalent binary values \(x_i \in {0, 1}\).

   • Relationships between variables must be reducible to quadratic (e.g., a QUBO) because the problem’s parameters are represented by qubits’ weights and couplers’ strengths on a QPU.

   • Formulations should be sparing in its number of variables because a QPU has a limited number of qubits and couplers.

   • Alternative formulations may have different implications for performance.

   Ocean demo applications, which formulate known problems, include:

   • Structural Imbalance.

   • Circuit-Fault Diagnosis.

Top-Down Approach

Another approach to envisioning how you can map your problem-solving process to Ocean software is to start from the top—your (possibly abstractly defined) problem—and work your way down the Ocean stack.

Ocean Software

Step	Description
State the Problem	Define your problem concretely/mathematically; for example, as a constraint satisfaction problem or a graph problem.
Formulate as a BQM	Reformulate an integer problem to use binary variables, for example, or convert a nonquadratic (high-order) polynomial to a QUBO. Ocean’s dwavebinarycsp and dwave_networkx can be helpful for some problems.
Decompose	Allocate large problems to classical and quantum resources. Ocean’s dwave-hybrid provides a framework and building blocks to help you create hybrid workflows.
Embed	Consider whether your problem has repeated elements, such as logic gates, when deciding what tool to use to minor-embed your BQM on the QPU. You might start with fully automated embedding (using EmbeddingComposite for example) and then seek performance improvements through minorminer.
Configure the QPU	Use spin-reversal transforms to reduce errors, for example, or examine the annealing with reverse anneal. See the system documents for more information of features that improve performance.