Large Map Coloring#
This example solves a map coloring problem to demonstrate an out-of-the-box use of
Ocean’s classical-quantum hybrid sampler, dwave-hybrid
KerberosSampler, that enables you to solve problems
of arbitrary structure and size.
Map coloring is an example of a constraint satisfaction problem (CSP). CSPs require that all a problem’s variables be assigned values, out of a finite domain, that result in the satisfying of all constraints. The map-coloring CSP is to assign a color to each region of a map such that any two regions sharing a border have different colors.
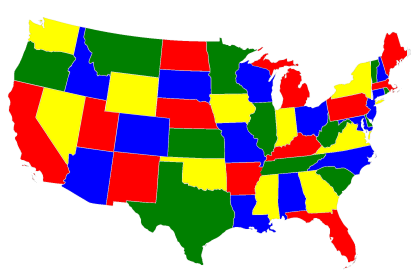
Coloring a map of the USA.#
The Map Coloring advanced example demonstrates lower-level coding of a similar problem, which gives the user more control over the solution procedure but requires the knowledge of some system parameters (e.g., knowing the maximum number of supported variables for the problem). Example Problem With Many Variables demonstrates the hybrid approach to problem solving in more detail by explicitly configuring the classical and quantum workflows.
Example Requirements#
The code in this example requires that your development environment have Ocean software and be configured to access SAPI, as described in the Initial Set Up section.
Solution Steps#
Section Workflow Steps: Formulation and Sampling describes the problem-solving workflow as consisting of two main steps: (1) Formulate the problem as an objective function in a supported model and (2) Solve your model with a D-Wave solver.
In this example, a function in Ocean software handles both steps. Our task is mainly to select the sampler used to solve the problem.
Formulate the Problem#
This example uses the NetworkX
read_adjlist() function to read a text file,
usa.adj, containing the states of the USA and their adjacencies (states with
a shared border) into a graph. The original map information was found on
write-only blog of Gregg Lind and looks like this:
# Author Gregg Lind
# License: Public Domain. I would love to hear about any projects you use if it for though!
#
AK,HI
AL,MS,TN,GA,FL
AR,MO,TN,MS,LA,TX,OK
AZ,CA,NV,UT,CO,NM
CA,OR,NV,AZ
CO,WY,NE,KS,OK,NM,AZ,UT
# Snipped here for brevity
You can see in the first non-comment line that the state of Alaska (“AK”) has Hawaii (“HI”) as an adjacency and that Alabama (“AL”) shares borders with four states.
>>> import networkx as nx
>>> G = nx.read_adjlist('usa.adj', delimiter = ',')
Graph G now represents states as vertices and each state’s neighbors as shared edges.
Solve the Problem by Sampling#
Ocean’s dwave_networkx can return a
minimum vertex coloring for a graph,
which assigns a color to the vertices of a graph in a way that no adjacent vertices
have the same color, using the minimum number of colors. Given a graph representing a
map and a sampler, the
min_vertex_coloring() function tries to
solve the map coloring problem.
dwave-hybrid KerberosSampler
is classical-quantum hybrid asynchronous decomposition sampler, which can decompose large problems
into smaller pieces that
it can run both classically (on your local machine) and on the D-Wave system.
Kerberos finds best samples by running in parallel TabuProblemSampler,
SimulatedAnnealingProblemSampler, and D-Wave subproblem sampling on
problem variables that have high impact. The only optional parameters set here
are a maximum number of iterations and number of iterations with no improvement that
terminates sampling. (See the Problem With Many Variables example for more details on configuring
the classical and quantum workflows.)
>>> import dwave_networkx as dnx
>>> from hybrid.reference.kerberos import KerberosSampler
>>> coloring = dnx.min_vertex_coloring(G, sampler=KerberosSampler(), chromatic_ub=4, max_iter=10, convergence=3)
>>> set(coloring.values())
{0, 1, 2, 3}
Note
The next code requires Matplotlib.
Plot the solution, if valid.
>>> import matplotlib.pyplot as plt
>>> node_colors = [coloring.get(node) for node in G.nodes()]
# Adjust the next line if using a different map
>>> if dnx.is_vertex_coloring(G, coloring):
... nx.draw(G, pos=nx.shell_layout(G, nlist = [list(G.nodes)[x:x+10] for x in range(0, 50, 10)] + [[list(G.nodes)[50]]]), with_labels=True, node_color=node_colors, node_size=400, cmap=plt.cm.rainbow)
>>> plt.show()
The graphic below shows the result of one such run.
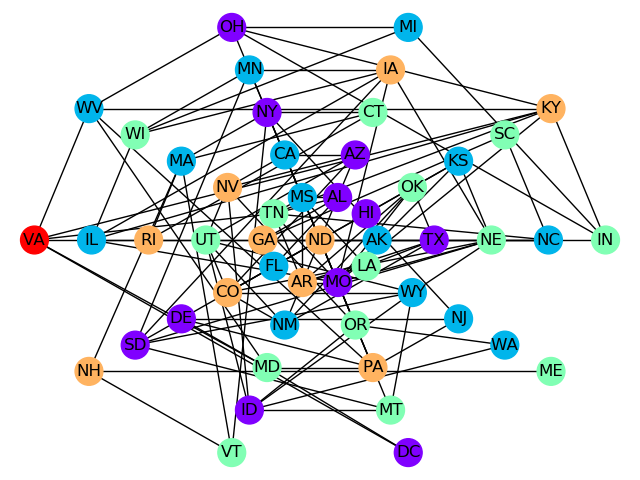
One solution found for the USA map-coloring problem.#