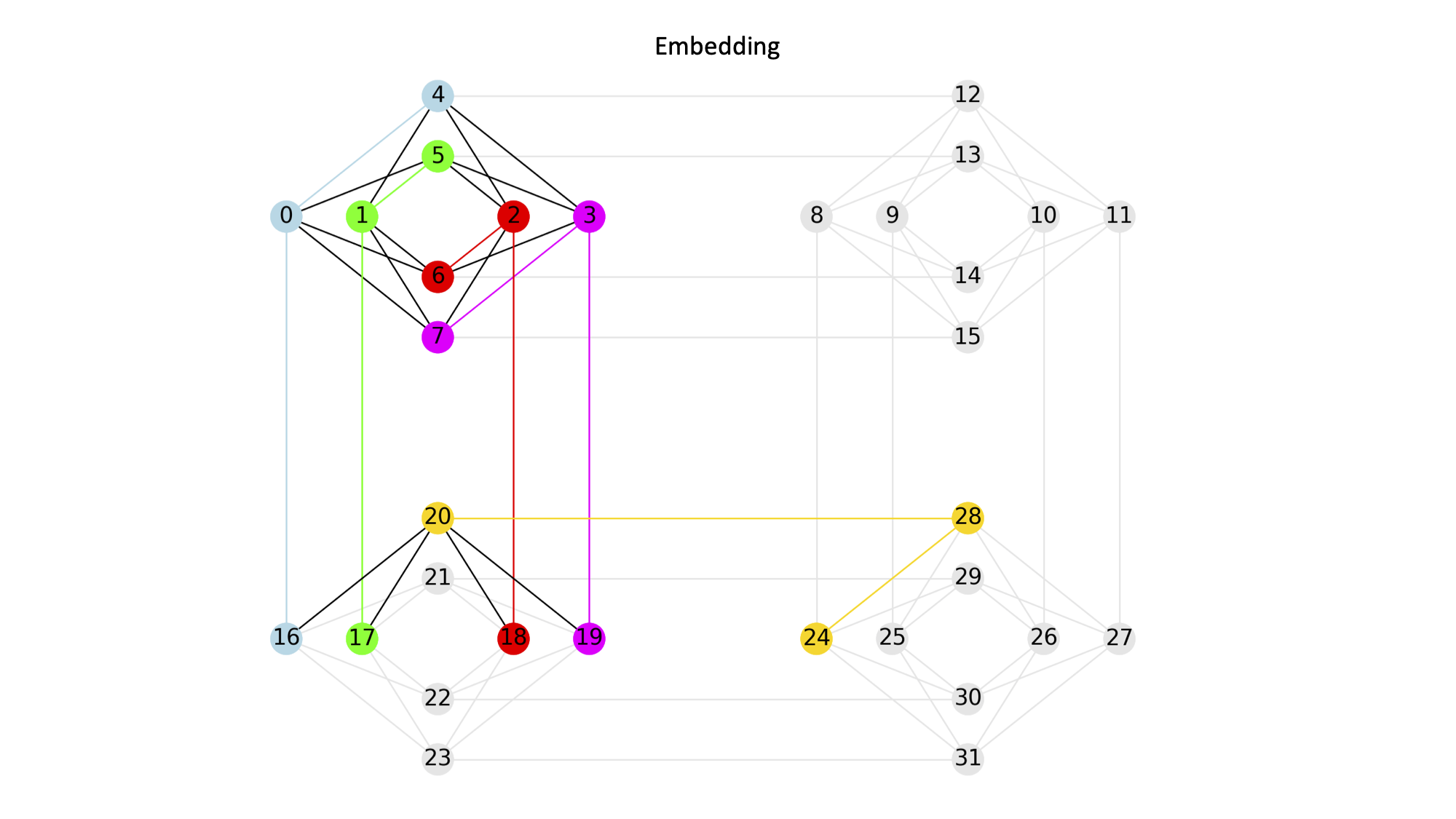
Clique Embedding#
If your source graph is a clique and your target graph is either a Chimera or
Pegasus graph, find_clique_embedding() may produce
better embeddings than the generic find_embedding() method.
- find_clique_embedding(nodes, g, seed=<object object>, use_cache=True)#
Finds a clique embedding in the graph
gusing a polynomial-time algorithm.- Parameters:
nodes (int/iterable) – A number (indicating the size of the desired clique) or an iterable (specifying the node labels of the desired clique).
g (NetworkX Graph) – The target graph that is either a
dwave_networkx.chimera_graph()ordwave_networkx.pegasus_graph().use_cache (bool, optional, default=True) – Whether or not to compute/restore a cache of clique embeddings for
g. Note that this function only uses the filesystem cache, and does not maintain the cache in memory. If many (or even several) embeddings are desired in a single session, it is recommended to usebusgraph_cache.seed (int, optional) – A seed for an internal random number generator. If
use_cacheis True, then the seed defaults to an internally-defined value which is consistent between runs. Otherwise, a seed is generated from the current python random state.
- Returns:
An embedding of node labels (either nodes, or range(nodes)) mapped to chains of a clique embedding.
- Return type:
Note
Due to internal optimizations, not all Chimera graphs are supported by this code. Specifically, the graphs
dwave_networkx.chimera_graph(m, n, t)()are only supported for \(t<=8\). The code currently supports D-Wave products, which have \(t=4\), but not all graphs. For graphs with \(t>8\), use the legacy chimera-embedding package.Note
When the cache is used, clique embeddings of all sizes are computed and cached. This takes somewhat longer than a single embedding, but tends to pay off after a fairly small number of calls. An exceptional use case is when there are a large number of missing internal couplers, where the result is nondeterministic – avoiding the cache in this case may be preferable.
Caching#
If multiple clique or biclique embeddings need to be computed for a single Chimera
or Pegasus graph, it may be more efficient to retrieve these embeddings through
the busgraph_cache, which creates LRU file-caches for the target graph’s
cliques and bicliques.
Class#
- class busgraph_cache(g, seed=0)#
A cache class for Chimera, Pegasus and Zephyr graphs, and their associated cliques and bicliques.
The cache files are stored in a directory determined by homebase (use
busgraph_cache.cache_rootdir()to retrieve the path to this directory). Subdirectories named cliques and bicliques are then created to store the respective caches in each.- Parameters:
g (NetworkX Graph) –
Note
Due to internal optimizations, not all Chimera graphs are supported by this code. Specifically, the graphs
dwave_networkx.chimera_graph(m, n, t)()are only supported for \(t<=8\). The code currently supports D-Wave products, which have \(t=4\), but not all graphs. For graphs with \(t>8\), use the legacy chimera-embedding package.
Methods#
|
Returns the directory corresponding to the provided cache version. |
Removes all caches created by this class, up to and including the current version. |
|
Returns a biclique embedding, minimizing the maximum chain length given its size. |
|
Returns a clique embedding, minimizing the maximum chainlength given its size. |
|
Returns the largest-size biclique where both sides have equal size. |
|
Returns the largest-found clique in the clique cache. |
|
Returns the largest-found clique in the clique cache, with a specified maximum |
Examples#
This example minor embeds a source clique of size 5 into a target Chimera graph.
from minorminer import busclique
import dwave_networkx as dnx
C = dnx.chimera_graph(2, 2)
embedding = busclique.find_clique_embedding(5, C)
print(embedding)
{0: (0, 16, 4), 1: (1, 17, 5), 2: (2, 18, 6), 3: (3, 19, 7), 4: (24, 20, 28)}