General Embedding

General embedding refers to embedding that may be useful for any type of graph.

The primary utility function, find_embedding(), is an implementation of the heuristic algorithm described in [1]. It accepts various optional parameters used to tune the algorithm’s execution or constrain the given problem.

This implementation performs on par with tuned, non-configurable implementations while providing users with hooks to easily use the code as a basic building block in research.

[1] https://arxiv.org/abs/1406.2741

Another function, find_clique_embedding(), can be used to find clique embeddings for Chimera, Pegasus, and Zephyr graphs in polynomial time. It is an implementation of the algorithm described in [2]. There are additional utilities for finding biclique embeddings as well.

[2] https://arxiv.org/abs/1507.04774

find_embedding(S, T, **params)

Heuristically attempt to find a minor-embedding of source graph S into a target graph T.

Parameters:

• S (iterable/NetworkX Graph) – The source graph as an iterable of label pairs representing the edges, or a NetworkX Graph.

• T (iterable/NetworkX Graph) – The target graph as an iterable of label pairs representing the edges, or a NetworkX Graph.

• **params (optional) – See below.

Returns:

When the optional parameter return_overlap is False (the default), the function returns a dict that maps labels in S to lists of labels in T. If the heuristic fails to find an embedding, an empty dictionary is returned.

When return_overlap is True, the function returns a tuple consisting of a dict that maps labels in S to lists of labels in T and a bool indicating whether or not a valid embedding was found.

When interrupted by Ctrl-C, the function returns the best embedding found so far.

Note that failure to return an embedding does not prove that no embedding exists.

Optional Parameters:

max_no_improvement (int, optional, default=10):

Maximum number of failed iterations to improve the current solution, where each iteration attempts to find an embedding for each variable of S such that it is adjacent to all its neighbours.

random_seed (int, optional, default=None):

Seed for the random number generator. If None, seed is set by os.urandom().

timeout (int, optional, default=1000):

Algorithm gives up after timeout seconds.

max_beta (double, optional, max_beta=None):

Qubits are assigned weight according to a formula (beta^n) where n is the number of chains containing that qubit. This value should never be less than or equal to 1. If None, max_beta is effectively infinite.

tries (int, optional, default=10):

Number of restart attempts before the algorithm stops. On D-WAVE 2000Q, a typical restart takes between 1 and 60 seconds.

inner_rounds (int, optional, default=None):

The algorithm takes at most this many iterations between restart attempts; restart attempts are typically terminated due to max_no_improvement. If None, inner_rounds is effectively infinite.

chainlength_patience (int, optional, default=10):

Maximum number of failed iterations to improve chain lengths in the current solution, where each iteration attempts to find an embedding for each variable of S such that it is adjacent to all its neighbours.

max_fill (int, optional, default=None):

Restricts the number of chains that can simultaneously incorporate the same qubit during the search. Values above 63 are treated as 63. If None, max_fill is effectively infinite.

threads (int, optional, default=1):

Maximum number of threads to use. Note that the parallelization is only advantageous where the expected degree of variables is significantly greater than the number of threads. Value must be greater than 1.

return_overlap (bool, optional, default=False):

This function returns an embedding, regardless of whether or not qubits are used by multiple variables. return_overlap determines the function’s return value. If True, a 2-tuple is returned, in which the first element is the embedding and the second element is a bool representing the embedding validity. If False, only an embedding is returned.

skip_initialization (bool, optional, default=False):

Skip the initialization pass. Note that this only works if the chains passed in through initial_chains and fixed_chains are semi-valid. A semi-valid embedding is a collection of chains such that every adjacent pair of variables (u,v) has a coupler (p,q) in the hardware graph where p is in chain(u) and q is in chain(v). This can be used on a valid embedding to immediately skip to the chain length improvement phase. Another good source of semi-valid embeddings is the output of this function with the return_overlap parameter enabled.

verbose (int, optional, default=0):

Level of output verbosity.

When set to 0:

Output is quiet until the final result.

When set to 1:

Output looks like this:

initialized
max qubit fill 3; num maxfull qubits=3
embedding trial 1
max qubit fill 2; num maxfull qubits=21
embedding trial 2
embedding trial 3
embedding trial 4
embedding trial 5
embedding found.
max chain length 4; num max chains=1
reducing chain lengths
max chain length 3; num max chains=5

When set to 2:

Output the information for lower levels and also report progress on minor statistics (when searching for an embedding, this is when the number of maxfull qubits decreases; when improving, this is when the number of max chains decreases).

When set to 3:

Report before each pass. Look here when tweaking tries, inner_rounds, and chainlength_patience.

When set to 4:

Report additional debugging information. By default, this package is built without this functionality. In the C++ headers, this is controlled by the CPPDEBUG flag.

Detailed explanation of the output information:

max qubit fill:

Largest number of variables represented in a qubit.

num maxfull:

Number of qubits that have max overfill.

max chain length:

Largest number of qubits representing a single variable.

num max chains:

Number of variables that have max chain size.

interactive (bool, optional, default=False):

If logging is None or False, the verbose output will be printed to stdout/stderr as appropriate, and keyboard interrupts will stop the embedding process and the current state will be returned to the user. Otherwise, output will be directed to the logger logging.getLogger(minorminer.__name__) and keyboard interrupts will be propagated back to the user. Errors will use logger.error(), verbosity levels 1 through 3 will use logger.info() and level 4 will use logger.debug().

initial_chains (dict, optional):

Initial chains inserted into an embedding before fixed_chains are placed, which occurs before the initialization pass. These can be used to restart the algorithm in a similar state to a previous embedding; for example, to improve chain length of a valid embedding or to reduce overlap in a semi-valid embedding (see skip_initialization) previously returned by the algorithm. Missing or empty entries are ignored. Each value in the dictionary is a list of qubit labels.

fixed_chains (dict, optional):

Fixed chains inserted into an embedding before the initialization pass. As the algorithm proceeds, these chains are not allowed to change, and the qubits used by these chains are not used by other chains. Missing or empty entries are ignored. Each value in the dictionary is a list of qubit labels.

restrict_chains (dict, optional):

Throughout the algorithm, it is guaranteed that chain[i] is a subset of restrict_chains[i] for each i, except those with missing or empty entries. Each value in the dictionary is a list of qubit labels.

suspend_chains (dict, optional):

This is a metafeature that is only implemented in the Python interface. suspend_chains[i] is an iterable of iterables; for example, suspend_chains[i] = [blob_1, blob_2], with each blob_j an iterable of target node labels.

This enforces the following:

for each suspended variable i,
    for each blob_j in the suspension of i,
        at least one qubit from blob_j will be contained in the chain for i

We accomplish this through the following problem transformation for each iterable blob_j in suspend_chains[i],

• Add an auxiliary node Zij to both source and target graphs

• Set fixed_chains[Zij] = [Zij]

• Add the edge (i,Zij) to the source graph

• Add the edges (q,Zij) to the target graph for each q in blob_j

---

Examples

This example minor embeds a triangular source K3 graph onto a square target graph.

from minorminer import find_embedding

# A triangle is a minor of a square.
triangle = [(0, 1), (1, 2), (2, 0)]
square = [(0, 1), (1, 2), (2, 3), (3, 0)]

# Find an assignment of sets of square variables to the triangle variables
embedding = find_embedding(triangle, square, random_seed=10)
print(len(embedding))  # 3, one set for each variable in the triangle
print(embedding)
# We don't know which variables will be assigned where, here are a
# couple possible outputs:
# [[0, 1], [2], [3]]
# [[3], [1, 0], [2]]

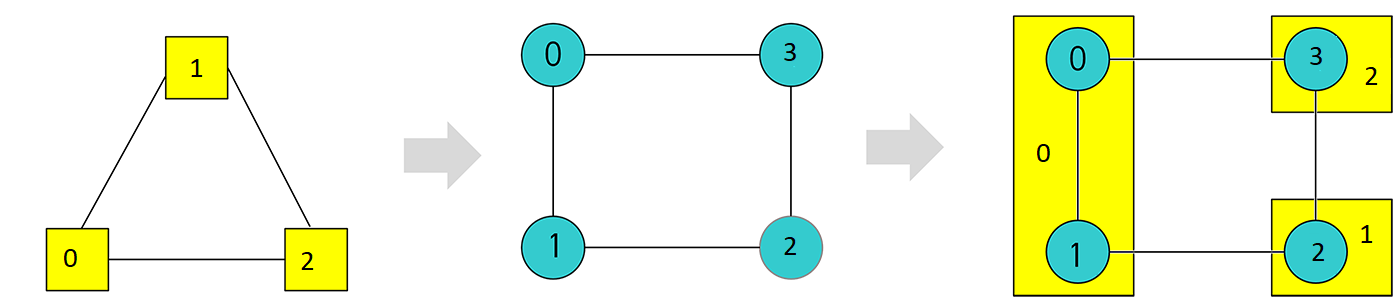
Embedding a \(K_3\) source graph into a square target graph by chaining two target nodes to represent one source node.

---

This minorminer execution of the example requires that source variable 0 always be assigned to target node 2.

embedding = find_embedding(triangle, square, fixed_chains={0: [2]})
print(embedding)
# [[2], [3, 0], [1]]
# [[2], [1], [0, 3]]
# And more, but all of them start with [2]

---

This minorminer execution of the example suggests that source variable 0 be assigned to target node 2 as a starting point for finding an embedding.

embedding = find_embedding(triangle, square, initial_chains={0: [2]})
print(embedding)
# [[2], [0, 3], [1]]
# [[0], [3], [1, 2]]
# Output where source variable 0 has switched to a different target node is possible.

---

This example minor embeds a fully connected K6 graph into a 30-node random regular graph of degree 3.

import networkx as nx

clique = nx.complete_graph(6).edges()
target_graph = nx.random_regular_graph(d=3, n=30).edges()

embedding = find_clique_embedding(clique, target_graph)

print(embedding)
# There are many possible outputs, and sometimes it might fail
# and return an empty list
# One run returned the following embedding:
{0: [10, 9, 19, 8],
1: [18, 7, 0, 12, 27],
2: [1, 17, 22],
3: [16, 28, 4, 21, 15, 23, 25],
4: [11, 24, 13],
5: [2, 14, 26, 5, 3]}

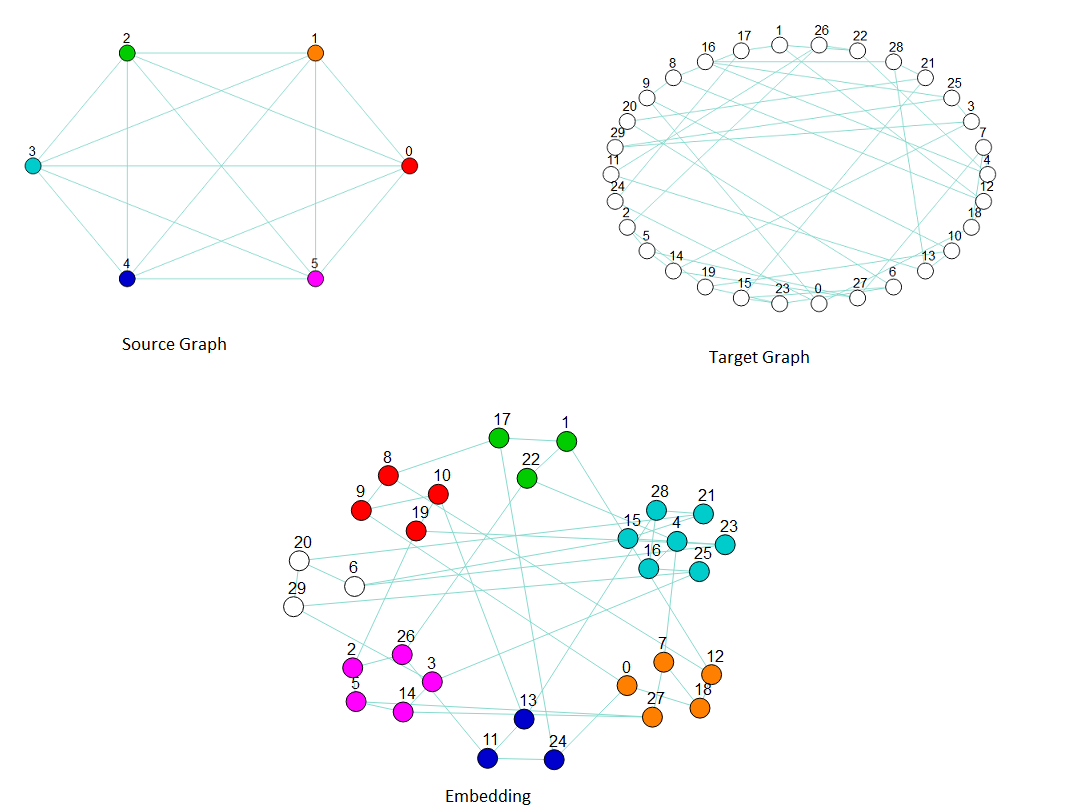
Embedding a \(K_6\) source graph (upper left) into a 30-node random target graph of degree 3 (upper right) by chaining several target nodes to represent one source node (bottom). The graphic of the embedding clusters chains representing nodes in the source graph: the cluster of red nodes is a chain of target nodes that represent source node 0, the orange nodes represent source node 1, and so on.