API for Samplers and Composites#
You can create your own samplers with dimod’s Sampler abstract base class (ABC)
providing complementary methods (e.g., ‘sample_qubo’ if only ‘sample_ising’ is implemented),
consistent responses, etc.
Properties of dimod Sampler Abstract Base Classes#
The following table describes the inheritance, properties, methods/mixins of sampler ABCs.
ABC |
Inherits from |
Abstract Properties |
Abstract Methods |
Mixin Methods |
|---|---|---|---|---|
at least one of
|
||||
at least one of
|
||||
|
|
The table shows, for example, that the Sampler class requires that you implement
the parameters and properties properties and at least
one sampler method; the class provides the unimplemented methods as mixins.
Creating a Sampler#
The Sampler abstract base class (abc) helps you create new
dimod samplers.
Any new dimod sampler must define a subclass of Sampler that implements
abstract properties parameters and properties
and one of the abstract methods sample(), sample_ising(),
or sample_qubo(). The Sampler class provides the complementary
methods as mixins and ensures consistent responses.
Implemented sample methods must accept, and warn on, unknown keyword arguments
**kwargs. This means that all implemented sample methods must have the
**kwargs parameter. remove_unknown_kwargs() is a convenience
method provided for this purpose.
For example, the following steps show how to easily create a dimod sampler. It is
sufficient to implement a single method (in this example the
sample_ising() method) to create a dimod sampler with the
Sampler class.
class LinearIsingSampler(dimod.Sampler):
def sample_ising(self, h, J, **kwargs):
kwargs = self.remove_unknown_kwargs(**kwargs)
sample = linear_ising(h, J)
energy = dimod.ising_energy(sample, h, J)
return dimod.SampleSet.from_samples([sample], vartype='SPIN', energy=[energy])
@property
def properties(self):
return dict()
@property
def parameters(self):
return dict()
For this example, the implemented sampler sample_ising() can be based on
a simple placeholder function, which returns a sample that minimizes the linear terms:
def linear_ising(h, J):
sample = {}
for v in h:
if h[v] < 0:
sample[v] = +1
else:
sample[v] = -1
return sample
The Sampler ABC provides the other sample methods “for free”
as mixins.
>>> sampler = LinearIsingSampler()
...
... # Implemented by class LinearIsingSampler:
>>> response = sampler.sample_ising({'a': -1}, {})
...
... # Mixins provided by Sampler class:
>>> sampleset = sampler.sample_qubo({('a', 'a'): 1})
>>> sampleset = sampler.sample(dimod.BinaryQuadraticModel.from_ising({'a': -1}, {}))
Below is a more complex version of the same sampler, where the
properties and parameters properties return
non-empty dicts.
class FancyLinearIsingSampler(dimod.Sampler):
def __init__(self):
self._properties = {'description': 'a simple sampler that only considers the linear terms'}
self._parameters = {'verbose': []}
def sample_ising(self, h, J, verbose=False, **kwargs):
kwargs = self.remove_unknown_kwargs(**kwargs)
sample = linear_ising(h, J)
energy = dimod.ising_energy(sample, h, J)
if verbose:
print(sample)
return dimod.SampleSet.from_samples([sample], energy=[energy])
@property
def properties(self):
return self._properties
@property
def parameters(self):
return self._parameters
- class Sampler[source]#
Abstract base class for dimod samplers.
Provides all methods
sample(),sample_ising(),sample_qubo()assuming at least one is implemented.Also includes utility method
remove_unknown_kwargs(), which may be used in sample methods to handle unknown kwargs.
Abstract Properties#
Parameters as a dict, where keys are keyword parameters accepted by the sampler methods and values are lists of the properties relevent to each parameter. |
|
Properties as a dict containing any additional information about the sampler. |
Mixin Methods#
|
Sample from a binary quadratic model. |
|
Sample from an Ising model using the implemented sample method. |
|
Sample from a QUBO using the implemented sample method. |
Methods#
|
Remove with warnings any keyword arguments not accepted by the sampler. |
Creating a Composed Sampler#
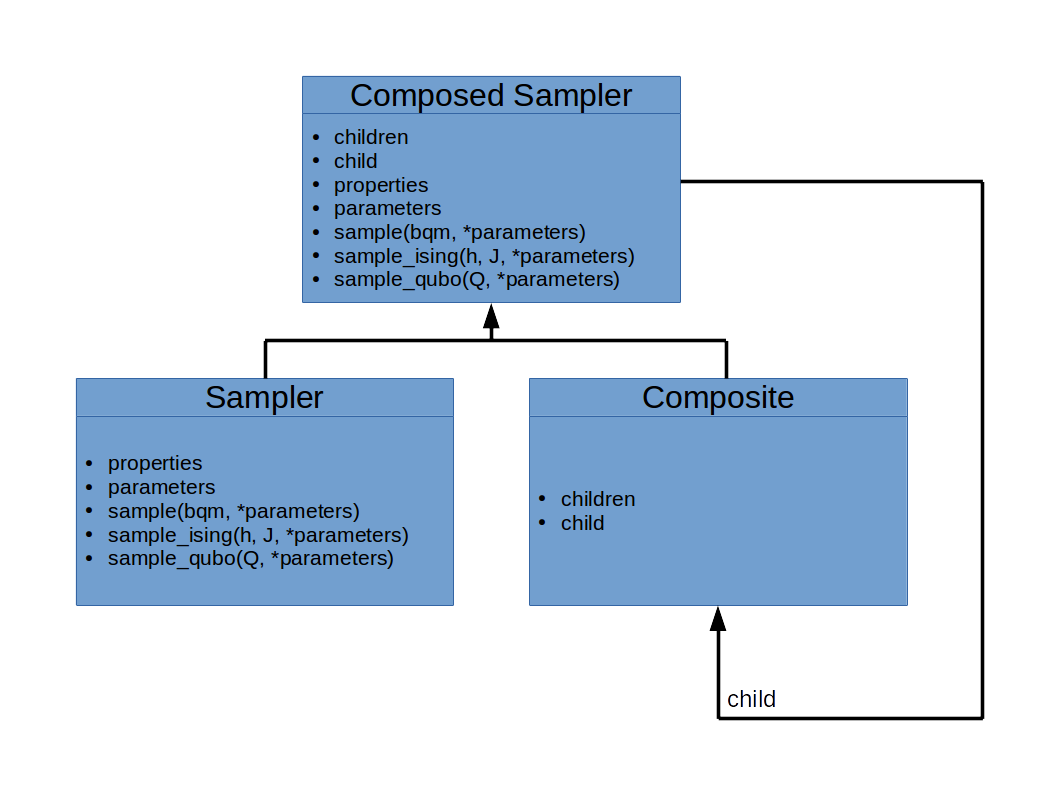
Composite Pattern#
Samplers can be composed. The composite pattern allows layers of pre- and post-processing to be applied to binary quadratic programs without needing to change the underlying sampler implementation.
We refer to these layers as composites. Each composed sampler must include at least one sampler, and possibly many composites.
Each composed sampler is itself a dimod sampler with all of the included methods and parameters. In this way complex samplers can be constructed.
The dimod ComposedSampler abstract base class inherits from Sampler class
its abstract methods, properties, and mixins (for example, a sample_Ising method) and from
Composite class the children property and child mixin (children being a list of
supported samplers with child providing the first).
Examples
The HigherOrderComposite
converts a binary quadratic model sampler to a binary polynomial sampler.
Given dimod sampler ExactSolver for example, the composed sampler is
used as any dimod sampler:
>>> sampler = dimod.ExactSolver()
>>> composed_sampler = dimod.HigherOrderComposite(sampler)
>>> J = {("a", "b", "c"): 1}
>>> sampleset = composed_sampler.sample_hising({}, J)
>>> set(sampleset.first.sample.values()) == {-1}
True
For more examples, see the source code for the composed documented in Composites.
- class Composite[source]#
Abstract base class for dimod composites.
Provides the
Composite.childmixin property and defines theComposite.childrenabstract property to be implemented. These define the supported samplers for the composed sampler.
Abstract Properties#
List of child samplers that that are used by this composite. |
Mixin Properties#
The child sampler. |
Creating a Structured Sampler#
A structured sampler can only sample from binary quadratic models with a specific graph.
For structured samplers you must implement the nodelist and
edgelist properties. The Structured abstract base
class provides access to the structure and
adjacency properties, the
to_networkx_graph() method, as well as any method or
properties required by the Sampler abstract base class. The
bqm_structured decorator verifies that any given binary quadratic model
conforms to the supported structure.
Examples
This simple example shows a structured sampler that can only sample from a binary quadratic model with two variables and one interaction.
class TwoVariablesSampler(dimod.Sampler, dimod.Structured):
@property
def nodelist(self):
return [0, 1]
@property
def edgelist(self):
return [(0, 1)]
@property
def properties(self):
return dict()
@property
def parameters(self):
return dict()
@dimod.decorators.bqm_structured
def sample(self, bqm):
# All bqm's passed in will be a subgraph of the sampler's structure
variable_list = list(bqm.linear)
samples = []
energies = []
for values in itertools.product(bqm.vartype.value, repeat=len(bqm)):
sample = dict(zip(variable_list, values))
samples.append(sample)
energies.append(bqm.energy(sample))
return dimod.SampleSet.from_samples(samples, bqm.vartype, energies)
return response
>>> import itertools
>>> sampler = TwoVariablesSampler()
>>> solutions = sampler.sample_ising({}, {(0, 1): -1})
>>> solutions.first.energy
-1.0
- class Structured[source]#
The abstract base class for dimod structured samplers.
Provides the
Structured.adjacencyandStructured.structureproperties, and theStructured.to_networkx_graph()method.Abstract properties
nodelistandedgelistmust be implemented.
Abstract Properties#
Nodes/variables allowed by the sampler. |
|
Edges/interactions allowed by the sampler. |
Mixin Properties#
Adjacency structure formatted as a dict, where keys are the nodes of the structured sampler and values are sets of all adjacent nodes for each key node. |
|
Structure of the structured sampler formatted as a |
Mixin Methods#
Convert structure to NetworkX graph format. |
Creating a Initialized Sampler#
Some samplers require or accept an initial starting point in sample-space.
See the source code for IdentitySampler for an example of using
this abstract base class in a sampler.
Mixin Methods#
|
Parse or generate initial states for an initialized sampler. |
Creating a Binary Polynomial Sampler#
Samplers that handle binary polynomials: problems with binary variables that are not constrained to quadratic interactions.
- class PolySampler[source]#
Sampler that supports binary polynomials.
Binary polynomials are an extension of binary quadratic models that allow higher-order interactions.
Abstract Properties#
A dict where keys are the keyword parameters accepted by the sampler methods and values are lists of the properties relevant to each parameter. |
|
A dict containing any additional information about the sampler. |
Abstract Methods#
|
Sample from a higher-order polynomial. |
Mixin Methods#
|
Sample from a higher-order Ising model. |
|
Sample from a higher-order unconstrained binary optimization problem. |
Creating a Composed Binary Polynomial Sampler#
- class ComposedPolySampler[source]#
Abstract base class for dimod composed polynomial samplers.
Inherits from
PolySamplerandComposite.