Coloring#
Graph coloring is the problem of assigning a color to the vertices of a graph in a way that no adjacent vertices have the same color.
Example#
The map-coloring problem is to assign a color to each region of a map (represented by a vertex on a graph) such that any two regions sharing a border (represented by an edge of the graph) have different colors.
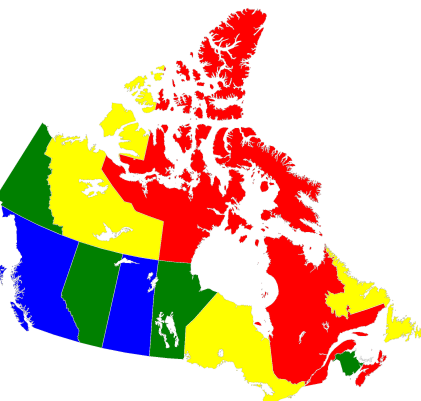
Coloring a map of Canada with four colors.#
|
Determines whether the given coloring is a vertex coloring of graph G. |
|
Returns an approximate minimum vertex coloring. |
|
Return a QUBO with ground states corresponding to a minimum vertex coloring. |
|
Returns an approximate vertex coloring. |
|
Return the QUBO with ground states corresponding to a vertex coloring. |