Coloring

Graph coloring is the problem of assigning a color to the vertices of a graph in a way that no adjacent vertices have the same color.

Example

The map-coloring problem is to assign a color to each region of a map (represented by a vertex on a graph) such that any two regions sharing a border (represented by an edge of the graph) have different colors.

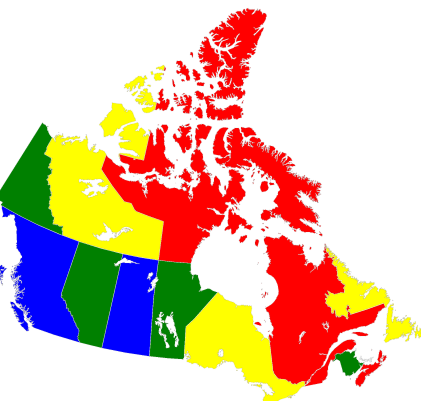
Coloring a map of Canada with four colors.

is_vertex_coloring(G, coloring)	Determines whether the given coloring is a vertex coloring of graph G.
min_vertex_color(G[, sampler, chromatic_lb, ...])	Returns an approximate minimum vertex coloring.
min_vertex_color_qubo(G[, chromatic_lb, ...])	Return a QUBO with ground states corresponding to a minimum vertex coloring.
vertex_color(G, colors[, sampler])	Returns an approximate vertex coloring.
vertex_color_qubo(G, colors)	Return the QUBO with ground states corresponding to a vertex coloring.