Layout Embedding#

minorminer.layout.find_embedding() offers a more specialized approach to find an embedding through the use of the Layout and Placement classes. This kind of embedding may be useful when the underlying data of your source graph is spatial. It can also be useful for embedding graphs with nodes of a low degree (i.e., a cubic graph).

find_embedding(S, T, layout=(<function p_norm>, None), placement=<function closest>, mm_hint_type='initial_chains', return_layouts=False, **kwargs)[source]#

Tries to embed S in T by computing layout-aware chains and passing them to minorminer.find_embedding(). Chains are passed as either initial_chains or suspend_chains (see documentation for minorminer.find_embedding() to learn more).

Parameters:

  • S (NetworkX Graph/edges data structure (dict, list, ...)) – The source graph being embedded or a NetworkX supported data structure for edges (see nx.convert.to_networkx_graph() for details).

  • T (NetworkX Graph/edges data structure (dict, list, ...)) – The target graph being embedded into or a NetworkX supported data structure for edges (see nx.convert.to_networkx_graph() for details).

  • layout (function/(function/dict/Layout, function/dict/Layout), optional) –

    A function to compute the Layout for both S and T, or a 2-tuple that either consists of a pair of functions or pre-computed layouts (in the form of Layout or dicts). The first entry in the 2-tuple applies to S while the second applies to T.

    Note

    If layout is a single function and T is a dnx_graph, then the function passed in is only applied to S and the dnx_layout is applied to T. To run a layout function explicitly on T, pass it in as a 2-tuple; i.e. (p_norm, p_norm).

  • placement (function/dict, optional, default=minorminer.placement.closest) –

    A function that uses the layouts of S and T to map the vertices of S to subsets of vertices of T (Placement), or a dict that contains the precomputed mapping/Placement.

    By default, closest() is called to compute placement.

  • mm_hint_type (str, optional, default="initial_chains") – This is the hint type passed to minorminer.find_embedding(). Supported types are “initial_chains” and “suspend_chains”. See minorminer.find_embedding() for more information.

  • return_layouts (bool, optional, default=False) – If True, layout objects of S and T are also returned.

  • **kwargs (dict) – Keyword arguments passed to Layout, Placement or minorminer.find_embedding().

Returns:

An embedding of vertices of S (keys) to chains in T (values). This embedding is dependent on the kwargs being passed in. If return_layouts is True, a 2-tuple is returned in which the first element is the embedding dict and the second element is another 2-tuple containing the source and target Layout objects.

Return type:

dict

Examples#

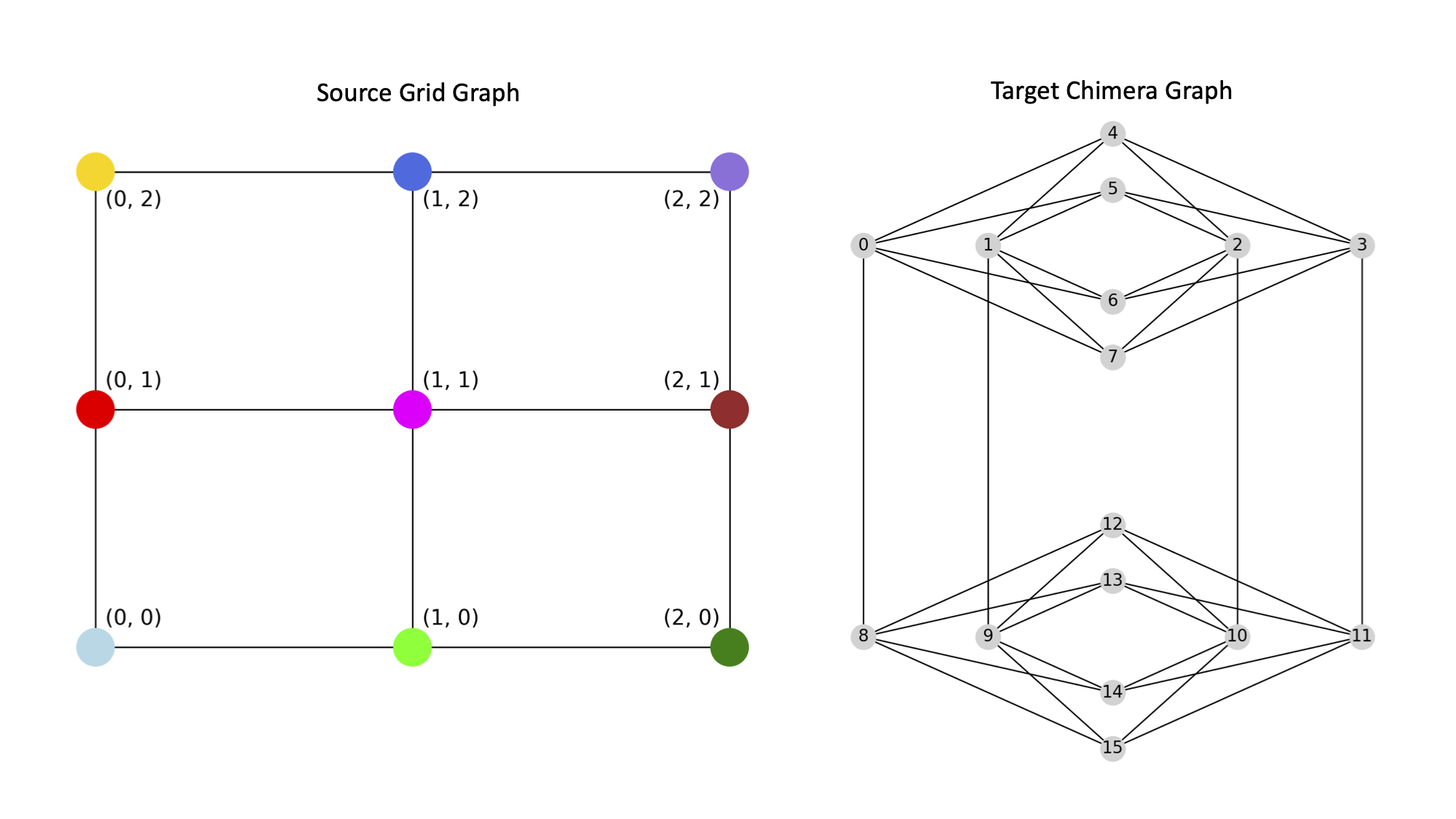
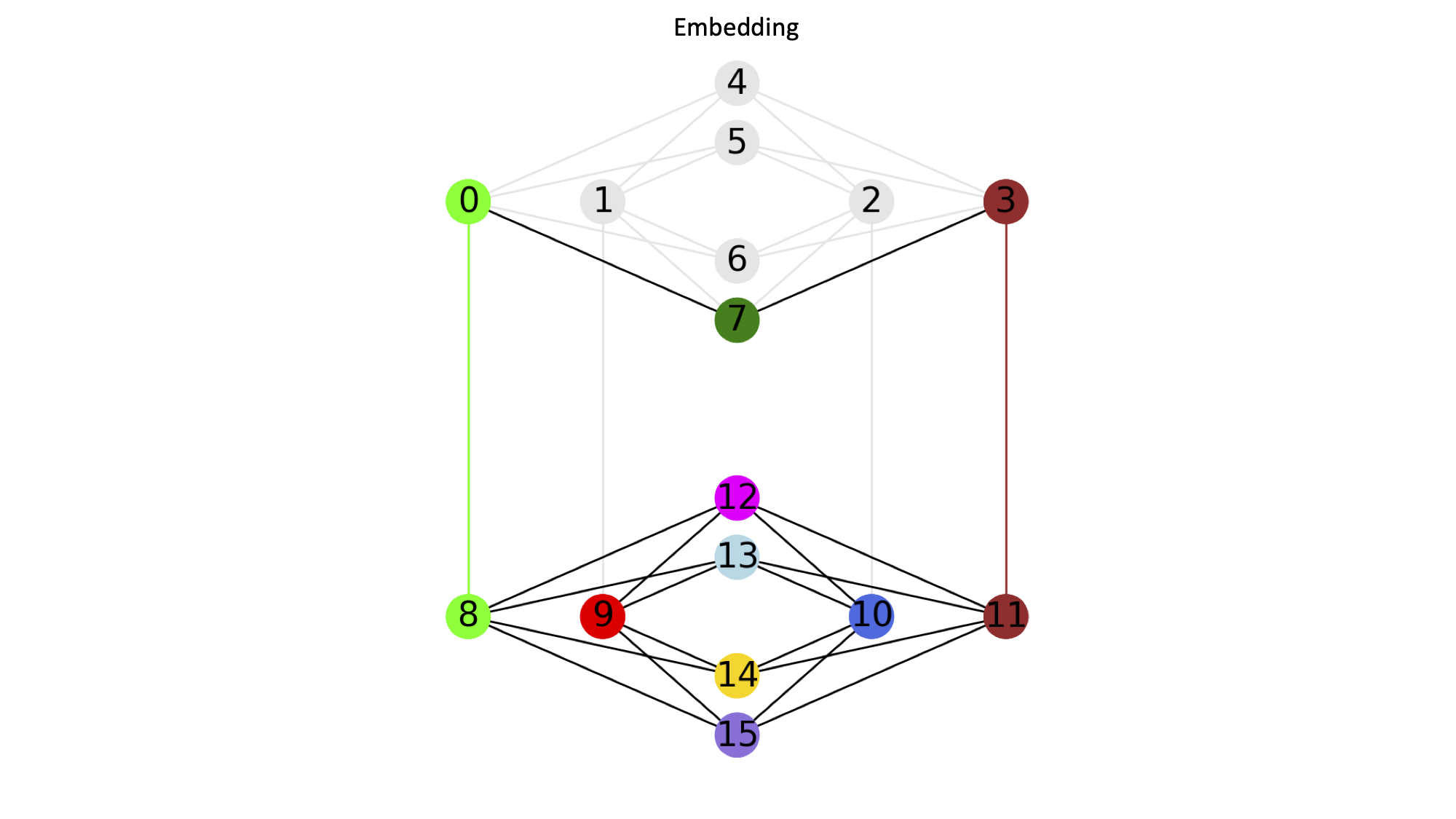
This example minor embeds a 3x3 grid graph onto a Chimera graph.

import networkx as nx
import dwave_networkx as dnx
import minorminer.layout as mml

grid_graph = nx.generators.lattice.grid_2d_graph(3, 3)
C = dnx.chimera_graph(2,1)

embedding = mml.find_embedding(grid_graph, C)
print(embedding)
# There are many possible outputs, and sometimes it might fail
# and return an empty list
# One run returned the following embedding:
{(0, 0): [13], (1, 0): [0, 8], (0, 1): [9], (1, 1): [12], (0, 2): [14], (1, 2): [10], (2, 0): [7], (2, 1): [11, 3], (2, 2): [15]}
Source 2-dimensional 3x3 grid graph and a target Chimera graph
Embedding a source 2-dimensional 3x3 grid graph onto a target Chimera graph

Layout#

class Layout(G, layout=None, dim=None, center=None, scale=None, pack_components=True, **kwargs)[source]#

Class that stores (or computes) coordinates in dimension dim for each node in graph G.

Parameters:

  • G (NetworkX Graph/edges data structure (dict, list, ...)) – The graph to compute the layout for or a NetworkX supported data structure for edges (see nx.convert.to_networkx_graph() for details).

  • layout (dict/function, optional, default=None) –

    If a dict, this specifies a pre-computed layout for G.

    If a function, this should be in the form of layout(G, **kwargs), in which dim, center, and scale are passed in as kwargs and the return value is a dict representing a layout of G.

    If None, nx.random_layout(G, **kwargs)() is called.

  • dim (int, optional, default=None) – The desired dimension of the computed layout, \(R^{\dim}\). If None, dim is set as the dimension of layout.

  • center (tuple, optional, default=None) – The desired center point of the computed layout. If None, center is set as the center of layout.

  • scale (float, optional, default=None) – The desired scale of the computed layout; i.e. the layout is in \([center - scale, center + scale]^d\) space. If None, scale is set to be the scale of layout.

  • pack_components (bool, optional, default=True) – If True, and if the graph contains multiple components and dim is None or 2, the components will be laid out individually and packed into a rectangle.

  • **kwargs (dict) – Keyword arguments are passed to layout if it is a function.

Functions for Creating Layouts#

p_norm(G, p=2, starting_layout=None, G_distances=None, dim=None, center=None, scale=None, **kwargs)[source]#

Embeds graph G in \(R^d\) with the p-norm and minimizes a Kamada-Kawai-esque objective function to achieve an embedding with low distortion.

This computes a Layout for G where the graph distance and the p-distance are very close to each other.

By default, p_norm() is used to compute the layout for source graphs when minorminer.layout.find_embedding() is called.

Parameters:

  • G (NetworkX Graph) – The graph to compute the layout for.

  • p (int, optional, default=2) – The order of the p-norm to use as a metric.

  • starting_layout (dict, optional, default=None) – A mapping from the vertices of G to points in \(R^d\). If None, nx.spectral_layout() is used if possible. Otherwise, nx.random_layout() is used.

  • G_distances (dict, optional, default=None) – A dictionary of dictionaries representing distances from every vertex in G to every other vertex in G. If None, it is computed.

  • dim (int, optional, default=None) – The desired dimension of the returned layout, \(R^{\dim}\). If None, the dimension of center is used. If center is None, dim is set to 2.

  • center (tuple, optional, default=None) – The desired center point of the returned layout. If None, center is set as the origin in \(R^{\dim}\) space.

  • scale (float, optional, default=None) – The desired scale of the returned layout; i.e. the layout is in \([center - scale, center + scale]^d\) space. If None, no scale is set.

Returns:

Layout.layout, a mapping from vertices of G (keys) to points in \(R^d\) (values).

Return type:

dict

Examples

This example creates a Layout object for a hexagonal lattice graph, with coordinates computed using p_norm().

>>> import networkx as nx
>>> import minorminer.layout as mml
...
>>> G = nx.hexagonal_lattice_graph(2,2)
>>> layout = mml.Layout(G, mml.p_norm, center=(1,1))

layout may be passed in directly to minorminer.layout.find_embedding().

Alternatively, p_norm() may be passed in instead.

This next example finds an embedding of a hexagonal lattice graph on a Chimera graph, in which the layouts of both the source and target graphs are computed using p_norm.

>>> import networkx as nx
>>> import dwave_networkx as dnx
>>> import minorminer.layout as mml
...
>>> G = nx.hexagonal_lattice_graph(2,2)
>>> C = dnx.chimera_graph(2,2)
>>> embedding = mml.find_embedding(G,
...                                C,
...                                layout=(mml.p_norm, mml.p_norm),
...                                center=(1,1))
dnx_layout(G, dim=None, center=None, scale=None, **kwargs)[source]#

The Chimera or Pegasus layout from dwave_networkx centered at the origin with scale as a function of the number of rows or columns. Note: As per the implementation of dnx.*_layout, if \(dim>2\), coordinates beyond the second are 0.

By default, dnx_layout() is used to compute the layout for target Chimera or Pegasus graphs when minorminer.layout.find_embedding() is called.

Parameters:

  • G (NetworkX Graph) – The graph to compute the layout for.

  • dim (int, optional, default=None) – The desired dimension of the returned layout, \(R^{\dim}\). If None, the dimension of center is used. If center is None, dim is set to 2.

  • center (tuple, optional, default=None) – The desired center point of the returned layout. If None, it is set as the origin in \(R^{\dim}\) space.

  • scale (float, optional, default=None) – The desired scale of the returned layout; i.e. the layout is in \([center - scale, center + scale]^d\) space. If None, it is set as \(max(n, m)/2\), where n, m are the number of columns, rows respectively in G.

Returns:

Layout.layout, a mapping from vertices of G (keys) to points in \(R^d\) (values).

Return type:

dict

Examples

This example creates a Layout object for a Pegasus graph, with coordinates computed using dnx_layout().

>>> import networkx as nx
>>> import minorminer.layout as mml
...
>>> P = dnx.pegasus_graph(4)
>>> layout = mml.Layout(P, mml.dnx_layout, center=(1,1), scale=2)

Placement#

class Placement(S_layout, T_layout, placement=None, scale_ratio=None, **kwargs)[source]#

Class that stores (or computes) a mapping of source nodes to collections of target nodes without any constraints. In mathematical terms, map V(S) to \(2^{V(T)}\).

Parameters:

  • S_layout (Layout) – A layout for S; i.e. a map from S to \(R^d\).

  • T_layout (Layout) – A layout for T; i.e. a map from T to \(R^d\).

  • placement (dict/function, optional, default=None) –

    If a dict, this specifies a pre-computed placement for S in T.

    If a function, the function is called on S_layout and T_layout, placement(S_layout, T_layout), and should return a dict representing a placement of S in T.

    If None, a random placement of S in T is selected.

  • scale_ratio (float, optional, default=None) – If None, S_layout is not scaled. Otherwise, S_layout is scaled to scale_ratio*T_layout.scale.

  • **kwargs (dict) – Keyword arguments are passed to placement if it is a function.

Functions for Creating Placements#

intersection(S_layout, T_layout, **kwargs)[source]#

Map each vertex of S to its nearest row/column intersection qubit in T (T must be a D-Wave hardware graph). Note: This will modify S_layout.

Parameters:

  • S_layout (Layout) – A layout for S; i.e. a map from S to R^d.

  • T_layout (Layout) – A layout for T; i.e. a map from T to R^d.

Returns:

A mapping from vertices of S (keys) to vertices of T (values).

Return type:

dict

Examples

This example creates a Placement object that stores a mapping computed with intersection(), in which the nodes from a source hexagonal lattice graph are mapped to a target Chimera graph.

>>> import networkx as nx
>>> import dwave_networkx as dnx
>>> import minorminer.layout as mml
...
>>> G = nx.hexagonal_lattice_graph(2,2)
>>> G_layout = mml.Layout(G, mml.p_norm)
>>> C = dnx.chimera_graph(2,2)
>>> C_layout = mml.Layout(C, mml.dnx_layout)
>>> placement = mml.Placement(G_layout, C_layout, placement=mml.intersection)

placement may be passed in directly to minorminer.layout.find_embedding().

Alternatively, intersection() may be passed in instead, as shown in the example below.

>>> import networkx as nx
>>> import dwave_networkx as dnx
>>> import minorminer.layout as mml
...
>>> G = nx.hexagonal_lattice_graph(2,2)
>>> C = dnx.chimera_graph(2,2)
>>> embedding = mml.find_embedding(G,
...                                C,
...                                placement=mml.intersection)
closest(S_layout, T_layout, subset_size=(1, 1), num_neighbors=1, **kwargs)[source]#

Maps vertices of S to the closest vertices of T as given by S_layout and T_layout. i.e. For each vertex u in S_layout and each vertex v in T_layout, map u to the v with minimum Euclidean distance \((||u - v||_2)\).

By default, closest() is used to compute the placement of an embedding when minorminer.layout.find_embedding() is called.

Parameters:

  • S_layout (Layout) – A layout for S; i.e. a map from S to \(R^d\).

  • T_layout (Layout) – A layout for T; i.e. a map from T to \(R^d\).

  • subset_size (tuple, optional, default=(1, 1)) – A lower (subset_size[0]) and upper (subset_size[1]) bound on the size of subsets of T that will be considered when mapping vertices of S.

  • num_neighbors (int, optional, default=1) – The number of closest neighbors to query from the KDTree–the neighbor with minimum overlap is chosen. Increasing this reduces overlap, but increases runtime.

Returns:

A mapping from vertices of S (keys) to subsets of vertices of T (values).

Return type:

dict

Examples

This example creates a Placement object that stores a mapping computed with closest(), in which the nodes from a source hexagonal lattice graph are mapped to a target Chimera graph.

>>> import networkx as nx
>>> import dwave_networkx as dnx
>>> import minorminer.layout as mml
...
>>> G = nx.hexagonal_lattice_graph(2,2)
>>> G_layout = mml.Layout(G, mml.p_norm)
>>> C = dnx.chimera_graph(2,2)
>>> C_layout = mml.Layout(C, mml.dnx_layout)
>>> placement = mml.Placement(G_layout, C_layout, placement=mml.closest)