Constraint Satisfaction#

A constraint satisfaction problem (CSP) requires that all the problem’s variables be assigned values, out of a finite domain, that result in the satisfying of all constraints.

The map-coloring CSP, for example, is to assign a color to each region of a map such that any two regions sharing a border have different colors.

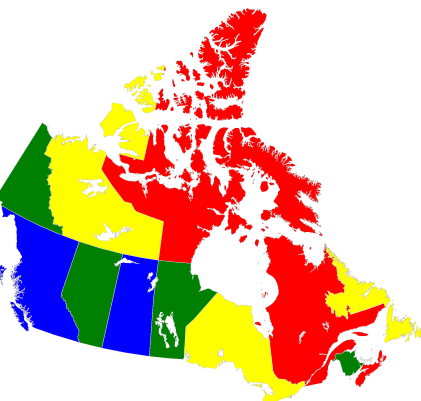
image

Coloring a map of Canada with four colors.#

The constraints for the map-coloring problem can be expressed as follows:

  • Each region is assigned one color only, of \(C\) possible colors.

  • The color assigned to one region cannot be assigned to adjacent regions.

A finite domain CSP consists of a set of variables, a specification of the domain of each variable, and a specification of the constraints over combinations of the allowed values of the variables. A constraint \(C_\alpha(\bf{x}_\alpha)\) defined over a subset of variables \(\bf{x}_\alpha\) defines the set of feasible and infeasible combinations of \(\bf{x}_\alpha\). The constraint \(C_\alpha\) may be be viewed as a predicate which evaluates to true on feasible configurations and to false on infeasible configurations. For example, if the domains of variables \(X_1,X_2,X_3\) are all \(\{0,1,2\}\), and the constraint is \(X_1+X_2<X_3\) then the feasible set is \(\{(0,0,1),(0,0,2),(0,1,2),(1,0,2)\}\), and all remaining combinations are infeasible.

Binary CSPs#

Solving such problems as the map-coloring CSP on a sampler such as the D-Wave system necessitates that the mathematical formulation use binary variables because the solution is implemented physically with qubits, and so must translate to spins \(s_i\in\{-1,+1\}\) or equivalent binary values \(x_i\in \{0,1\}\). This means that in formulating the problem by stating it mathematically, you might use unary encoding to represent the \(C\) colors: each region is represented by \(C\) variables, one for each possible color, which is set to value \(1\) if selected, while the remaining \(C-1\) variables are \(0\).

Another example is logical circuits. Logic gates such as AND, OR, NOT, XOR etc can be viewed as binary CSPs: the mathematically expressed relationships between binary inputs and outputs must meet certain validity conditions. For inputs \(x_1,x_2\) and output \(y\) of an AND gate, for example, the constraint to satisfy, \(y=x_1x_2\), can be expressed as a set of valid configurations: (0, 0, 0), (0, 1, 0), (1, 0, 0), (1, 1, 1), where the variable order is \((x_1, x_2, y)\).

Boolean AND Operation#

\(x_1,x_2\)

\(y\)

\(0,0\)

\(0\)

\(0,1\)

\(0\)

\(1,0\)

\(0\)

\(1,1\)

\(1\)

You can use Ocean’s dwavebinarycsp to construct a BQM from a CSP. It maps each individual constraint in the CSP to a ‘small’ Ising model or QUBO, in a mapping called a penalty model.

For more information on using the D-Wave system to solve CSPs, see the following documentation: